Orbital Hybridisation
History and uses
Chemist Linus Pauling first developed the hybridisation theory in 1931 to explain the structure of simple molecules such as methane (CH4) using atomic orbitals. Pauling pointed out that a carbon atom forms four bonds by using one s and three p orbitals, so that "it might be inferred" that a carbon atom would form three bonds at right angles (using p orbitals) and a fourth weaker bond using the s orbital in some arbitrary direction. In reality, methane has four C–H bonds of equivalent strength. The angle between any two bonds is the tetrahedral bond angle of 109°28' (around 109.5°). Pauling supposed that in the presence of four hydrogen atoms, the s and p orbitals form four equivalent combinations which he called hybrid orbitals. Each hybrid is denoted sp to indicate its composition, and is directed along one of the four C–H bonds. This concept was developed for such simple chemical systems, but the approach was later applied more widely, and today it is considered an effective heuristic for rationalizing the structures of organic compounds. It gives a simple orbital picture equivalent to Lewis structures.
Hybridisation theory is an integral part of organic chemistry, one of the most compelling examples being Baldwin's rules. For drawing reaction mechanisms sometimes a classical bonding picture is needed with two atoms sharing two electrons. Hybridisation theory explains bonding in alkenes and methane. The amount of p character or s character, which is decided mainly by orbital hybridisation, can be used to reliably predict molecular properties such as acidity or basicity.
Overview
Orbitals are a model representation of the behavior of electrons within molecules. In the case of simple hybridization, this approximation is based on atomic orbitals, similar to those obtained for the hydrogen atom, the only neutral atom for which the Schrödinger equation can be solved exactly. In heavier atoms, such as carbon, nitrogen, and oxygen, the atomic orbitals used are the 2s and 2p orbitals, similar to excited state orbitals for hydrogen.
Hybrid orbitals are assumed to be mixtures of atomic orbitals, superimposed on each other in various proportions. For example, in methane, the C hybrid orbital which forms each carbon–hydrogen bond consists of 25% s character and 75% p character and is thus described as sp (read as s-p-three) hybridised. Quantum mechanics describes this hybrid as an sp wavefunction of the form , where N is a normalisation constant (here 1/2) and pσ is a p orbital directed along the C-H axis to form a sigma bond. The ratio of coefficients (denoted λ in general) is in this example. Since the electron density associated with an orbital is proportional to the square of the wavefunction, the ratio of p-character to s-character is λ = 3. The p character or the weight of the p component is Nλ = 3/4.
Types of hybridisation
sp

Hybridisation describes the bonding of atoms from an atom's point of view. For a tetrahedrally coordinated carbon (e.g., methane CH4), the carbon should have 4 orbitals directed towards the 4 hydrogen atoms.
Carbon's ground state configuration is 1s 2s 2p or more easily read:
| C | ↑↓ | ↑↓ | ↑ | ↑ | |
| 1s | 2s | 2p | 2p | 2p |
This diagram suggests that the carbon atom could use its two singly occupied p-type orbitals to form two covalent bonds with two hydrogen atoms in a methylene (CH2) molecule, with a hypothetical bond angle of 90° corresponding to the angle between two p orbitals on the same atom. However the true H–C–H angle in singlet methylene is about 102° which implies the presence of some orbital hybridisation.
The carbon atom can also bond to four hydrogen atoms in methane by an excitation (or promotion) of an electron from the doubly occupied 2s orbital to the empty 2p orbital, producing four singly occupied orbitals.
| C* | ↑↓ | ↑ | ↑ | ↑ | ↑ |
| 1s | 2s | 2p | 2p | 2p |
The energy released by the formation of two additional bonds more than compensates for the excitation energy required, energetically favoring the formation of four C-H bonds.
According to quantum mechanics the lowest energy is obtained if the four bonds are equivalent, which requires that they are formed from equivalent orbitals on the carbon. A set of four equivalent orbitals can be obtained that are linear combinations of the valence-shell (core orbitals are almost never involved in bonding) s and p wave functions, which are the four sp hybrids.
| C* | ↑↓ | ↑ | ↑ | ↑ | ↑ |
| 1s | sp | sp | sp | sp |
In CH4, four sp hybrid orbitals are overlapped by hydrogen 1s orbitals, yielding four σ (sigma) bonds (that is, four single covalent bonds) of equal length and strength.
The following :
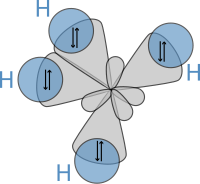
translates into :
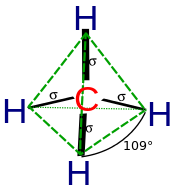
sp


Other carbon compounds and other molecules may be explained in a similar way. For example, ethene (C2H4) has a double bond between the carbons.
For this molecule, carbon sp hybridises, because one π (pi) bond is required for the double bond between the carbons and only three σ bonds are formed per carbon atom. In sp hybridisation the 2s orbital is mixed with only two of the three available 2p orbitals, usually denoted 2px and 2py. The third 2p orbital (2pz) remains unhybridised.
| C* | ↑↓ | ↑ | ↑ | ↑ | ↑ |
| 1s | sp | sp | sp | 2p |
forming a total of three sp orbitals with one remaining p orbital. In ethene, the two carbon atoms form a σ bond by overlapping one sp orbital from each carbon atom. The π bond between the carbon atoms perpendicular to the molecular plane is formed by 2p–2p overlap. Each carbon atom forms covalent C–H bonds with two hydrogens by s–sp overlap, all with 120° bond angles. The hydrogen–carbon bonds are all of equal strength and length, in agreement with experimental data.
sp

The chemical bonding in compounds such as alkynes with triple bonds is explained by sp hybridization. In this model, the 2s orbital is mixed with only one of the three p orbitals,
| C* | ↑↓ | ↑ | ↑ | ↑ | ↑ |
| 1s | sp | sp | 2p | 2p |
resulting in two sp orbitals and two remaining p orbitals. The chemical bonding in acetylene (ethyne) (C2H2) consists of sp–sp overlap between the two carbon atoms forming a σ bond and two additional π bonds formed by p–p overlap. Each carbon also bonds to hydrogen in a σ s–sp overlap at 180° angles.
Hybridisation and molecule shape

Hybridisation helps to explain molecule shape, since the angles between bonds are approximately equal to the angles between hybrid orbitals. This is in contrast to valence shell electron-pair repulsion (VSEPR) theory, which can be used to predict molecular geometry based on empirical rules rather than on valence-bond or orbital theories.
sp hybridisation
As the valence orbitals of main group elements are the one s and three p orbitals with the corresponding octet rule, sp hybridization is used to model the shape of these molecules.
| Coordination number | Shape | Hybridisation | Examples |
|---|---|---|---|
| 2 | Linear | sp hybridisation (180°) | CO2 |
| 3 | Trigonal planar | sp hybridisation (120°) | BCl3 |
| 4 | Tetrahedral | sp hybridisation (109.5°) | CCl4 |
| Interorbital angles | |||
spd hybridisation
As the valence orbitals of transition metals are the five d, one s and three p orbitals with the corresponding 18-electron rule, spd hybridisation is used to model the shape of these molecules. These molecules tend to have multiple shapes corresponding to the same hybridization due to the different d-orbitals involved. A square planar complex has one unoccupied p-orbital and hence has 16 valence electrons.
| Coordination number | Shape | Hybridisation | Examples |
|---|---|---|---|
| 4 | Square planar | spd hybridisation | PtCl4 |
| 5 | Trigonal bipyramidal | spd hybridisation | Fe(CO)5 |
| Square pyramidal | MnCl5 | ||
| 6 | Octahedral | spd hybridisation | Mo(CO)6 |
| 7 | Pentagonal bipyramidal | spd hybridisation | ZrF7 |
| Capped octahedral | MoF7 | ||
| Capped trigonal prismatic | TaF7 | ||
| 8 | Square antiprismatic | spd hybridisation | ReF8 |
| Dodecahedral | Mo(CN)8 | ||
| Bicapped trigonal prismatic | ZrF8 | ||
| 9 | Tricapped trigonal prismatic | spd hybridisation | ReH9 |
| Capped square antiprismatic |
sd hybridisation
In certain transition metal complexes with a low d electron count, the p-orbitals are unoccupied and sd hybridisation is used to model the shape of these molecules.
| Coordination number | Shape | Hybridisation | Examples |
|---|---|---|---|
| 3 | Trigonal pyramidal | sd hybridisation (90°) | CrO3 |
| 4 | Tetrahedral | sd hybridisation (70.5°, 109.5°) | TiCl4 |
| 5 | Square pyramidal | sd hybridisation (65.9°, 114.1°) | Ta(CH3)5 |
| 6 | C3v Trigonal prismatic | sd hybridisation (63.4°, 116.6°) | W(CH3)6 |
| Interorbital angles | |||
Hybridisation of hypervalent molecules
Octet expansion
In some general chemistry textbooks, hybridization is presented for main group coordination number 5 and above using an "expanded octet" scheme with d-orbitals first proposed by Pauling. However, such a scheme is now considered to be incorrect in light of computational chemistry calculations.
| Coordination number | Molecular shape | Hybridisation | Examples |
|---|---|---|---|
| 5 | Trigonal bipyramidal | spd hybridisation | PF5 |
| 6 | Octahedral | spd hybridisation | SF6 |
| 7 | Pentagonal bipyramidal | spd hybridisation | IF7 |
In 1990, Eric Alfred Magnusson of the University of New South Wales published a paper definitively excluding the role of d-orbital hybridisation in bonding in hypervalent compounds of second-row (period 3) elements, ending a point of contention and confusion. Part of the confusion originates from the fact that d-functions are essential in the basis sets used to describe these compounds (or else unreasonably high energies and distorted geometries result). Also, the contribution of the d-function to the molecular wavefunction is large. These facts were incorrectly interpreted to mean that d-orbitals must be involved in bonding.
Resonance
In light of computational chemistry, a better treatment would be to invoke sigma bond resonance in addition to hybridisation, which implies that each resonance structure has its own hybridisation scheme. All resonance structures must obey the octet rule.
| Coordination number | Resonance structures |
|---|---|
| 5 | Trigonal bipyramidal |

| |
| 6 | Octahedral |

| |
| 7 | Pentagonal bipyramidal |
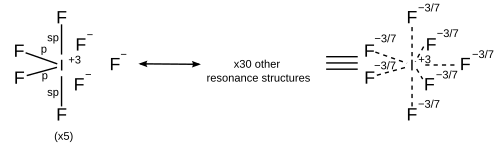
|
Hybridisation in computational VB theory
While the simple model of orbital hybridisation is commonly used to explain molecular shape, hybridisation is used differently when computed in modern valence bond programs. Specifically, hybridisation is not determined a priori but is instead variationally optimized to find the lowest energy solution and then reported. This means that all artificial constraints, specifically two constraints, on orbital hybridisation are lifted:
- that hybridisation is restricted to integer values (isovalent hybridisation)
- that hybrid orbitals are orthogonal to one another (hybridisation defects)
This means that in practice, hybrid orbitals do not conform to the simple ideas commonly taught and thus in scientific computational papers are simply referred to as sp, spd or sd hybrids to express their nature instead of more specific integer values.
Isovalent hybridisation
Although ideal hybrid orbitals can be useful, in reality, most bonds require orbitals of intermediate character. This requires an extension to include flexible weightings of atomic orbitals of each type (s, p, d) and allows for a quantitative depiction of the bond formation when the molecular geometry deviates from ideal bond angles. The amount of p-character is not restricted to integer values; i.e., hybridizations like sp are also readily described.
The hybridization of bond orbitals is determined by Bent's rule: "Atomic s character concentrates in orbitals directed towards electropositive substituents".
For molecules with lone pairs, the bonding orbitals are isovalent sp hybrids. For example, the two bond-forming hybrid orbitals of oxygen in water can be described as sp to give the interorbital angle of 104.5°. This means that they have 20% s character and 80% p character and does not imply that a hybrid orbital is formed from one s and four p orbitals on oxygen since the 2p subshell of oxygen only contains three p orbitals.
Hybridisation defects
Hybridisation of s and p orbitals to form effective sp hybrids requires that they have comparable radial extent. While 2p orbitals are on average less than 10% larger than 2s, in part attributable to the lack of a radial node in 2p orbitals, 3p orbitals which have one radial node, exceed the 3s orbitals by 20–33%. The difference in extent of s and p orbitals increases further down a group. The hybridisation of atoms in chemical bonds can be analysed by considering localised molecular orbitals, for example using natural localised molecular orbitals in a natural bond orbital (NBO) scheme. In methane, CH4, the calculated p/s ratio is approximately 3 consistent with "ideal" sp hybridisation, whereas for silane, SiH4, the p/s ratio is closer to 2. A similar trend is seen for the other 2p elements. Substitution of fluorine for hydrogen further decreases the p/s ratio. The 2p elements exhibit near ideal hybridisation with orthogonal hybrid orbitals. For heavier p block elements this assumption of orthogonality cannot be justified. These deviations from the ideal hybridisation were termed hybridisation defects by Kutzelnigg.
However, computational VB groups such as Gerratt, Cooper and Raimondi (SCVB) as well as Shaik and Hiberty (VBSCF) go a step further to argue that even for model molecules such as methane, ethylene and acetylene, the hybrid orbitals are already defective and nonorthogonal, with hybridisations such as sp instead of sp for methane.
Photoelectron spectra
One misconception concerning orbital hybridization is that it incorrectly predicts the ultraviolet photoelectron spectra of many molecules. While this is true if Koopmans' theorem is applied to localized hybrids, quantum mechanics requires that the (in this case ionized) wavefunction obey the symmetry of the molecule which implies resonance in valence bond theory. For example, in methane, the ionised states (CH4) can be constructed out of four resonance structures attributing the ejected electron to each of the four sp orbitals. A linear combination of these four structures, conserving the number of structures, leads to a triply degenerate T2 state and an A1 state. The difference in energy between each ionized state and the ground state would be ionization energy, which yields two values in agreement with experimental results.

Localized vs canonical molecular orbitals
Bonding orbitals formed from hybrid atomic orbitals may be considered as localized molecular orbitals, which can be formed from the delocalized orbitals of molecular orbital theory by an appropriate mathematical transformation. For molecules in the ground state, this transformation of the orbitals leaves the total many-electron wave function unchanged. The hybrid orbital description of the ground state is, therefore equivalent to the delocalized orbital description for ground state total energy and electron density, as well as the molecular geometry that corresponds to the minimum total energy value.
Two localized representations
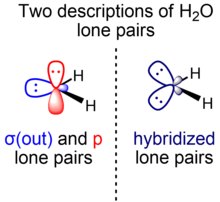
Molecules with multiple bonds or multiple lone pairs can have orbitals represented in terms of sigma and pi symmetry or equivalent orbitals. Different valence bond methods use either of the two representations, which have mathematically equivalent total many-electron wave functions and are related by a unitary transformation of the set of occupied molecular orbitals.
For multiple bonds, the sigma-pi representation is the predominant one compared to the equivalent orbital (bent bond) representation. In contrast, for multiple lone pairs, most textbooks use the equivalent orbital representation. However, the sigma-pi representation is also used, such as by Weinhold and Landis within the context of natural bond orbitals, a localized orbital theory containing modernized analogs of classical (valence bond/Lewis structure) bonding pairs and lone pairs. For the hydrogen fluoride molecule, for example, two F lone pairs are essentially unhybridized p orbitals, while the other is an sp hybrid orbital. An analogous consideration applies to water (one O lone pair is in a pure p orbital, another is in an sp hybrid orbital).
See also
- Crystal field theory
- Isovalent hybridisation
- Ligand field theory
- Linear combination of atomic orbitals
- MO diagrams
- VALBOND
References
- ^ Housecroft, Catherine E.; Sharpe, Alan G. (2005). Inorganic Chemistry (2nd ed.). Pearson Prentice-Hal. p. 100. ISBN 0130-39913-2.
- ^ Pauling, L. (1931), "The nature of the chemical bond. Application of results obtained from the quantum mechanics and from a theory of paramagnetic susceptibility to the structure of molecules", Journal of the American Chemical Society, 53 (4): 1367–1400, doi:10.1021/ja01355a027
- ^ Brittin, W. E. (1945). "Valence Angle of the Tetrahedral Carbon Atom". J. Chem. Educ. 22 (3): 145. Bibcode:1945JChEd..22..145B. doi:10.1021/ed022p145.
- ^ L. Pauling The Nature of the Chemical Bond (3rd ed., Oxford University Press 1960) p.111–120.
- ^ Clayden, Jonathan; Greeves, Nick; Warren, Stuart; Wothers, Peter (2001). Organic Chemistry (1st ed.). Oxford University Press. p. 105. ISBN 978-0-19-850346-0.
- ^ Organic Chemistry, Third Edition Marye Anne Fox James K. Whitesell 2003 ISBN 978-0-7637-3586-9
- ^ Organic Chemistry 3rd Ed. 2001 Paula Yurkanis Bruice ISBN 978-0-130-17858-9
- ^ "Acids and Bases". Orgo Made Simple. Archived from the original on February 4, 2015. Retrieved 23 June 2015.
- ^ Isaiah Shavitt (1985), Geometry and singlet-triplet energy gap in methylene: A critical review of experimental and theoretical determinations. Tetrahedron, volume 41, issue 8, page 1531 doi:10.1016/S0040-4020(01)96393-8
- ^ McMurray, J. (1995). Chemistry Annotated Instructors Edition (4th ed.). Prentice Hall. p. 272. ISBN 978-0-131-40221-8
- ^ Gillespie, R.J. (2004), "Teaching molecular geometry with the VSEPR model", Journal of Chemical Education, 81 (3): 298–304, Bibcode:2004JChEd..81..298G, doi:10.1021/ed081p298
- ^ Weinhold, Frank; Landis, Clark R. (2005). Valency and bonding: A Natural Bond Orbital Donor-Acceptor Perspective. Cambridge: Cambridge University Press. pp. 367, 374–376, 381–383. ISBN 978-0-521-83128-4.
- ^ Bayse, Craig; Hall, Michael (1999). "Prediction of the Geometries of Simple Transition Metal Polyhydride Complexes by Symmetry Analysis". J. Am. Chem. Soc. 121 (6): 1348–1358. doi:10.1021/ja981965+.
- ^ Kaupp, Martin (2001). ""Non-VSEPR" Structures and Bonding in d(0) Systems". Angew Chem Int Ed Engl. 40 (1): 3534–3565. doi:10.1002/1521-3773(20011001)40:19<3534::AID-ANIE3534>3.0.CO;2-#. PMID 11592184.
- ^ Magnusson, E. (1990). "Hypercoordinate molecules of second-row elements: d functions or d orbitals?". J. Am. Chem. Soc. 112 (22): 7940–7951. doi:10.1021/ja00178a014.
- ^ David L. Cooper; Terry P. Cunningham; Joseph Gerratt; Peter B. Karadakov; Mario Raimondi (1994). "Chemical Bonding to Hypercoordinate Second-Row Atoms: d Orbital Participation versus Democracy". Journal of the American Chemical Society. 116 (10): 4414–4426. doi:10.1021/ja00089a033.
- ^ Richard D. Harcourt; Thomas M. Klapötke (2003). "Increased valence (qualitative valence bond) descriptions of the electronic structures of electron-rich fluorine-containing molecules". Journal of Fluorine Chemistry. 123 (1): 5–20. doi:10.1016/S0022-1139(03)00012-5.
- ^ Frenking, Gernot; Shaik, Sason, eds. (2014). "Chapter 3: The NBO View of Chemical Bonding". The Chemical Bond: Fundamental Aspects of Chemical Bonding. John Wiley & Sons. ISBN 978-3-527-66471-9.
- ^ Kaupp, Martin (2007). "The role of radial nodes of atomic orbitals for chemical bonding and the periodic table". Journal of Computational Chemistry. 28 (1): 320–325. doi:10.1002/jcc.20522. ISSN 0192-8651. PMID 17143872. S2CID 12677737.
- ^ Kaupp, Martin (2014) [1st. Pub. 2014]. "Chapter 1: Chemical bonding of main group elements". In Frenking, Gernod & Shaik, Sason (eds.). The Chemical Bond: Chemical Bonding Across the Periodic Table. Wiley-VCH. ISBN 9781234567897.
- ^ Kutzelnigg, W. (August 1988). "Orthogonal and non-orthogonal hybrids". Journal of Molecular Structure: THEOCHEM. 169: 403–419. doi:10.1016/0166-1280(88)80273-2.
- ^ Shaik, Sason; Danovich, David; Hiberty, Philippe (2022). "On the nature of the chemical bond in valence bond theory". The Journal of Chemical Physics. 157 (9): 090901. doi:10.1063/5.0095953. PMID 36075734.
- ^ Andrei M. Tokmachev; Andrei L. Tchougreeff; Igor A. Misurkin (2001). "Ionization potentials within semiempirical antisymmetrized product of strictly localized geminals approach". International Journal of Quantum Chemistry. 85 (3): 109–117. doi:10.1002/qua.1060.
- ^ Sason S. Shaik; Phillipe C. Hiberty (2008). A Chemist's Guide to Valence Bond Theory. New Jersey: Wiley-Interscience. pp. 104–106. ISBN 978-0-470-03735-5.
- ^ Weinhold, Frank; Landis, Clark R. (2012). Discovering Chemistry with Natural Bond Orbitals. Hoboken, N.J.: Wiley. pp. 67–68. ISBN 978-1-118-11996-9.



