Portal:Mathematics : Soft.lk - A Premium Software Developers - Meet one of the most powerful and intuitive POS systems for retail in Sri Lanka

21 Aug, 2019
By, Wikipedia

Portal:Mathematics

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Refresh with new selections below (purge)

Featured articles – load new batch

Featured articles are displayed here, which represent some of the best content on English Wikipedia.

Image 1
The weighing pans of this balance scale contain zero objects, divided into two equal groups.

In mathematics, zero is an even number. In other words, its parity—the quality of an integer being even or odd—is even. This can be easily verified based on the definition of "even": zero is an integer multiple of 2, specifically 0 × 2. As a result, zero shares all the properties that characterize even numbers: for example, 0 is neighbored on both sides by odd numbers, any decimal integer has the same parity as its last digit—so, since 10 is even, 0 will be even, and if $y$ is even then $y + x$ has the same parity as $x$ —indeed, $0 + x$ and $x$ always have the same parity.

Zero also fits into the patterns formed by other even numbers. The parity rules of arithmetic, such as even − even = even, require 0 to be even. Zero is the additive identity element of the group of even integers, and it is the starting case from which other even natural numbers are recursively defined. Applications of this recursion from graph theory to computational geometry rely on zero being even. Not only is 0 divisible by 2, it is divisible by every power of 2, which is relevant to the binary numeral system used by computers. In this sense, 0 is the "most even" number of all. (Full article...)
Image 2
Logic studies valid forms of inference like modus ponens.

Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the study of deductively valid inferences or logical truths. It examines how conclusions follow from premises based on the structure of arguments alone, independent of their topic and content. Informal logic is associated with informal fallacies, critical thinking, and argumentation theory. Informal logic examines arguments expressed in natural language whereas formal logic uses formal language. When used as a countable noun, the term "a logic" refers to a specific logical formal system that articulates a proof system. Logic plays a central role in many fields, such as philosophy, mathematics, computer science, and linguistics.

Logic studies arguments, which consist of a set of premises that leads to a conclusion. An example is the argument from the premises "it's Sunday" and "if it's Sunday then I don't have to work" leading to the conclusion "I don't have to work". Premises and conclusions express propositions or claims that can be true or false. An important feature of propositions is their internal structure. For example, complex propositions are made up of simpler propositions linked by logical vocabulary like $\land$ (and) or $\to$ (if...then). Simple propositions also have parts, like "Sunday" or "work" in the example. The truth of a proposition usually depends on the meanings of all of its parts. However, this is not the case for logically true propositions. They are true only because of their logical structure independent of the specific meanings of the individual parts. (Full article...)
Image 3

Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist. He is known for the work he did in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, and in particle physics, for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.

Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)
Image 4

Marian Adam Rejewski (Polish: [ˈmarjan rɛˈjɛfskʲi] ; 16 August 1905 – 13 February 1980) was a Polish mathematician and cryptologist who in late 1932 reconstructed the sight-unseen German military Enigma cipher machine, aided by limited documents obtained by French military intelligence.

Over the next nearly seven years, Rejewski and fellow mathematician-cryptologists Jerzy Różycki and Henryk Zygalski, working at the Polish General Staff's Cipher Bureau, developed techniques and equipment for decrypting the Enigma ciphers, even as the Germans introduced modifications to their Enigma machines and encryption procedures. Rejewski's contributions included the cryptologic card catalog and the cryptologic bomb. (Full article...)

In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as

\sum _{n=1}^{m}n(-1)^{n-1}.

The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:

1-2+3-4+\cdots ={\frac {1}{4}}.

(Full article...)

Leonhard Euler (/ˈɔɪlər/ OY-lər; German: [ˈleːɔnhaʁt ˈʔɔʏlɐ] , Swiss Standard German: [ˈleːɔnhart ˈɔʏlər]; 15 April 1707 – 18 September 1783) was a Swiss mathematician, physicist, astronomer, geographer, logician, and engineer who founded the studies of graph theory and topology and made pioneering and influential discoveries in many other branches of mathematics such as analytic number theory, complex analysis, and infinitesimal calculus. He introduced much of modern mathematical terminology and notation, including the notion of a mathematical function. He is also known for his work in mechanics, fluid dynamics, optics, astronomy, and music theory.

Euler is regarded as one of the greatest, most prolific mathematicians in history and the greatest of the 18th century. Several great mathematicians who produced their work after Euler's death have recognised his importance in the field as shown by quotes attributed to many of them: Pierre-Simon Laplace expressed Euler's influence on mathematics by stating, "Read Euler, read Euler, he is the master of us all." Carl Friedrich Gauss wrote: "The study of Euler's works will remain the best school for the different fields of mathematics, and nothing else can replace it." His 866 publications and his correspondence are being collected in the Opera Omnia Leonhard Euler which, when completed, will consist of 81 quartos. He spent most of his adult life in Saint Petersburg, Russia, and in Berlin, then the capital of Prussia. (Full article...)

$Image 7 Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because the remainder EA is less than DC. EA now measures (twice) the shorter length DC, with remainder FC shorter than EA. Then FC measures (three times) length EA. Because there is no remainder, the process ends with FC being the GCD. On the right Nicomachus's example with numbers 49 and 21 resulting in their GCD of 7 (derived from Heath 1908:300). In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC). It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules, and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations. The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as 252 = 21 × 12 and 105 = 21 × 5), and the same number 21 is also the GCD of 105 and 252 − 105 = 147. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example, 21 = 5 × 105 + (−2) × 252). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)$

In mathematics, the Euclidean algorithm, or Euclid's algorithm, is an efficient method for computing the greatest common divisor (GCD) of two integers (numbers), the largest number that divides them both without a remainder. It is named after the ancient Greek mathematician Euclid, who first described it in his Elements (c. 300 BC).
It is an example of an algorithm, a step-by-step procedure for performing a calculation according to well-defined rules,
and is one of the oldest algorithms in common use. It can be used to reduce fractions to their simplest form, and is a part of many other number-theoretic and cryptographic calculations.

The Euclidean algorithm is based on the principle that the greatest common divisor of two numbers does not change if the larger number is replaced by its difference with the smaller number. For example, 21 is the GCD of 252 and 105 (as

252 = 21 \times 12

and

105 = 21 \times 5)

, and the same number 21 is also the GCD of 105 and

252 - 105 = 147

. Since this replacement reduces the larger of the two numbers, repeating this process gives successively smaller pairs of numbers until the two numbers become equal. When that occurs, that number is the GCD of the original two numbers. By reversing the steps or using the extended Euclidean algorithm, the GCD can be expressed as a linear combination of the two original numbers, that is the sum of the two numbers, each multiplied by an integer (for example,

21 = 5 \times 105 + (-2) \times 252

). The fact that the GCD can always be expressed in this way is known as Bézout's identity. (Full article...)

Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.

Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)

An actuary is a professional with advanced mathematical skills who deals with the measurement and management of risk and uncertainty. These risks can affect both sides of the balance sheet and require asset management, liability management, and valuation skills. Actuaries provide assessments of financial security systems, with a focus on their complexity, their mathematics, and their mechanisms. The name of the corresponding academic discipline is actuarial science.

While the concept of insurance dates to antiquity, the concepts needed to scientifically measure and mitigate risks have their origins in the 17th century studies of probability and annuities. Actuaries of the 21st century require analytical skills, business knowledge, and an understanding of human behavior and information systems to design programs that manage risk, by determining if the implementation of strategies proposed for mitigating potential risks, does not exceed the expected cost of those risks actualized. The steps needed to become an actuary, including education and licensing, are specific to a given country, with various additional requirements applied by regional administrative units; however, almost all processes impart universal principles of risk assessment, statistical analysis, and risk mitigation, involving rigorously structured training and examination schedules, taking many years to complete. (Full article...)

$Image 10 The number π (/paɪ/; spelled out as "pi") is a mathematical constant that is the ratio of a circle's circumference to its diameter, approximately equal to 3.14159. The number π appears in many formulae across mathematics and physics. It is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as '"`UNIQ--postMath-00000008-QINU`"' are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an equation involving only finite sums, products, powers, and integers. The transcendence of π implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of π appear to be randomly distributed, but no proof of this conjecture has been found. For thousands of years, mathematicians have attempted to extend their understanding of π, sometimes by computing its value to a high degree of accuracy. Ancient civilizations, including the Egyptians and Babylonians, required fairly accurate approximations of π for practical computations. Around 250 BC, the Greek mathematician Archimedes created an algorithm to approximate π with arbitrary accuracy. In the 5th century AD, Chinese mathematicians approximated π to seven digits, while Indian mathematicians made a five-digit approximation, both using geometrical techniques. The first computational formula for π, based on infinite series, was discovered a millennium later. The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by the Welsh mathematician William Jones in 1706. (Full article...)$

The number $π$ (/paɪ/; spelled out as "pi") is a mathematical constant that is the ratio of a circle's circumference to its diameter, approximately equal to 3.14159. The number

π

appears in many formulae across mathematics and physics. It is an irrational number, meaning that it cannot be expressed exactly as a ratio of two integers, although fractions such as

{\tfrac {22}{7}}

are commonly used to approximate it. Consequently, its decimal representation never ends, nor enters a permanently repeating pattern. It is a transcendental number, meaning that it cannot be a solution of an equation involving only finite sums, products, powers, and integers. The transcendence of

π

implies that it is impossible to solve the ancient challenge of squaring the circle with a compass and straightedge. The decimal digits of

π

appear to be randomly distributed, but no proof of this conjecture has been found.

For thousands of years, mathematicians have attempted to extend their understanding of

π

, sometimes by computing its value to a high degree of accuracy. Ancient civilizations, including the Egyptians and Babylonians, required fairly accurate approximations of

π

for practical computations. Around 250 BC, the Greek mathematician Archimedes created an algorithm to approximate

π

with arbitrary accuracy. In the 5th century AD, Chinese mathematicians approximated

π

to seven digits, while Indian mathematicians made a five-digit approximation, both using geometrical techniques. The first computational formula for

π

, based on infinite series, was discovered a millennium later. The earliest known use of the Greek letter π to represent the ratio of a circle's circumference to its diameter was by the Welsh mathematician William Jones in 1706. (Full article...)

High-precision test of general relativity by the *Cassini* space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.

By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)

$Image 12 Portrait by August Köhler, c. 1910, after 1627 original Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ⓘ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium. Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein. Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. (Full article...)$

Johannes Kepler (/ˈkɛplər/; German: [joˈhanəs ˈkɛplɐ, -nɛs -] ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of planetary motion, and his books Astronomia nova, Harmonice Mundi, and Epitome Astronomiae Copernicanae, influencing among others Isaac Newton, providing one of the foundations for his theory of universal gravitation. The variety and impact of his work made Kepler one of the founders and fathers of modern astronomy, the scientific method, natural and modern science. He has been described as the "father of science fiction" for his novel Somnium.

Kepler was a mathematics teacher at a seminary school in Graz, where he became an associate of Prince Hans Ulrich von Eggenberg. Later he became an assistant to the astronomer Tycho Brahe in Prague, and eventually the imperial mathematician to Emperor Rudolf II and his two successors Matthias and Ferdinand II. He also taught mathematics in Linz, and was an adviser to General Wallenstein.
Additionally, he did fundamental work in the field of optics, being named the father of modern optics, in particular for his Astronomiae pars optica. He also invented an improved version of the refracting telescope, the Keplerian telescope, which became the foundation of the modern refracting telescope, while also improving on the telescope design by Galileo Galilei, who mentioned Kepler's discoveries in his work. (Full article...)

In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.

Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)

Emery Molyneux (/ˈɛməri ˈmɒlɪnoʊ/ EM-ər-ee MOL-in-oh; died June 1598) was an English Elizabethan maker of globes, mathematical instruments and ordnance. His terrestrial and celestial globes, first published in 1592, were the first to be made in England and the first to be made by an Englishman.

Molyneux was known as a mathematician and maker of mathematical instruments such as compasses and hourglasses. He became acquainted with many prominent men of the day, including the writer Richard Hakluyt and the mathematicians Robert Hues and Edward Wright. He also knew the explorers Thomas Cavendish, Francis Drake, Walter Raleigh and John Davis. Davis probably introduced Molyneux to his own patron, the London merchant William Sanderson, who largely financed the construction of the globes. When completed, the globes were presented to Elizabeth I. Larger globes were acquired by royalty, noblemen and academic institutions, while smaller ones were purchased as practical navigation aids for sailors and students. The globes were the first to be made in such a way that they were unaffected by the humidity at sea, and they came into general use on ships. (Full article...)

Algebra is the branch of mathematics that studies certain abstract systems, known as algebraic structures, and the manipulation of statements within those systems. It is a generalization of arithmetic that introduces variables and algebraic operations other than the standard arithmetic operations such as addition and multiplication.

Elementary algebra is the main form of algebra taught in school and examines mathematical statements using variables for unspecified values. It seeks to determine for which values the statements are true. To do so, it uses different methods of transforming equations to isolate variables. Linear algebra is a closely related field that investigates linear equations and combinations of them called systems of linear equations. It provides methods to find the values that solve all equations in the system at the same time, and to study the set of these solutions. (Full article...)

More featured articles

edit

Selected image – show another

animation showing a roughly star-shaped graph being traced out as a smaller circle rolls around inside of a larger circle

Hypotrochoid

Credit: Sam Derbyshire

A hypotrochoid is a curve traced out by a point "attached" to a smaller circle rolling around inside a fixed larger circle. In this example, the hypotrochoid is the red curve that is traced out by the red point 5 units from the center of the black circle of radius 3 as it rolls around inside the blue circle of radius 5. A special case is a hypotrochoid with the inner circle exactly one-half the radius of the outer circle, resulting in an ellipse (see an animation showing this). Mathematical analysis of closely-related curves called hypocycloids lead to special Lie groups. Both hypotrochoids and epitrochoids (where the moving circle rolls around on the outside of the fixed circle) can be created using the Spirograph drawing toy. These curves have applications in the "real world" in epicyclic and hypocycloidal gearing, which were used in World War II in the construction of portable radar gear and may be used today in 3D printing.

More selected pictures

Good articles – load new batch

These are Good articles, which meet a core set of high editorial standards.

Image 1
Composite numbers can be arranged into rectangles but prime numbers cannot.

A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.

The property of being prime is called primality. A simple but slow method of checking the primality of a given number $n$ , called trial division, tests whether $n$ is a multiple of any integer between 2 and ${\sqrt {n}}$ . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always produces the correct answer in polynomial time but is too slow to be practical. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of October 2024 the largest known prime number is a Mersenne prime with 41,024,320 decimal digits. (Full article...)
Image 2
In mathematics, a free abelian group is an abelian group with a basis. Being an abelian group means that it is a set with an addition operation that is associative, commutative, and invertible. A basis, also called an integral basis, is a subset such that every element of the group can be uniquely expressed as an integer combination of finitely many basis elements. For instance the two-dimensional integer lattice forms a free abelian group, with coordinatewise addition as its operation, and with the two points (1,0) and (0,1) as its basis. Free abelian groups have properties which make them similar to vector spaces, and may equivalently be called free $\mathbb {Z}$ -modules, the free modules over the integers. Lattice theory studies free abelian subgroups of real vector spaces. In algebraic topology, free abelian groups are used to define chain groups, and in algebraic geometry they are used to define divisors.

The elements of a free abelian group with basis $B$ may be described in several equivalent ways. These include formal sums over $B$ , which are expressions of the form ${\textstyle \sum a_{i}b_{i}}$ where each $a_{i}$ is a nonzero integer, each $b_{i}$ is a distinct basis element, and the sum has finitely many terms. Alternatively, the elements of a free abelian group may be thought of as signed multisets containing finitely many elements of $B$ , with the multiplicity of an element in the multiset equal to its coefficient in the formal sum.
Another way to represent an element of a free abelian group is as a function from $B$ to the integers with finitely many nonzero values; for this functional representation, the group operation is the pointwise addition of functions. (Full article...)
$Image 3 Huygens by Caspar Netscher (1671), Museum Boerhaave, Leiden Christiaan Huygens, Lord of Zeelhem, FRS (/ˈhaɪɡənz/ HY-gənz, US also /ˈhɔɪɡənz/ HOY-gənz; Dutch: [ˈkrɪstijaːn ˈɦœyɣə(n)s] ⓘ; also spelled Huyghens; Latin: Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution. In physics, Huygens made seminal contributions to optics and mechanics, while as an astronomer he studied the rings of Saturn and discovered its largest moon, Titan. As an engineer and inventor, he improved the design of telescopes and invented the pendulum clock, the most accurate timekeeper for almost 300 years. A talented mathematician and physicist, his works contain the first idealization of a physical problem by a set of mathematical parameters, and the first mathematical and mechanistic explanation of an unobservable physical phenomenon. Huygens first identified the correct laws of elastic collision in his work De Motu Corporum ex Percussione, completed in 1656 but published posthumously in 1703. In 1659, Huygens derived geometrically the formula in classical mechanics for the centrifugal force in his work De vi Centrifuga, a decade before Newton. In optics, he is best known for his wave theory of light, which he described in his Traité de la Lumière (1690). His theory of light was initially rejected in favour of Newton's corpuscular theory of light, until Augustin-Jean Fresnel adapted Huygens's principle to give a complete explanation of the rectilinear propagation and diffraction effects of light in 1821. Today this principle is known as the Huygens–Fresnel principle. (Full article...)$

Image 3

Christiaan Huygens, Lord of Zeelhem, FRS (/ˈhaɪɡənz/ HY-gənz, US also /ˈhɔɪɡənz/ HOY-gənz; Dutch: [ˈkrɪstijaːn ˈɦœyɣə(n)s] ; also spelled Huyghens; Latin: Hugenius; 14 April 1629 – 8 July 1695) was a Dutch mathematician, physicist, engineer, astronomer, and inventor who is regarded as a key figure in the Scientific Revolution. In physics, Huygens made seminal contributions to optics and mechanics, while as an astronomer he studied the rings of Saturn and discovered its largest moon, Titan. As an engineer and inventor, he improved the design of telescopes and invented the pendulum clock, the most accurate timekeeper for almost 300 years. A talented mathematician and physicist, his works contain the first idealization of a physical problem by a set of mathematical parameters, and the first mathematical and mechanistic explanation of an unobservable physical phenomenon.

Huygens first identified the correct laws of elastic collision in his work De Motu Corporum ex Percussione, completed in 1656 but published posthumously in 1703. In 1659, Huygens derived geometrically the formula in classical mechanics for the centrifugal force in his work De vi Centrifuga, a decade before Newton. In optics, he is best known for his wave theory of light, which he described in his Traité de la Lumière (1690). His theory of light was initially rejected in favour of Newton's corpuscular theory of light, until Augustin-Jean Fresnel adapted Huygens's principle to give a complete explanation of the rectilinear propagation and diffraction effects of light in 1821. Today this principle is known as the Huygens–Fresnel principle. (Full article...)

Fredrik Carl Mülertz Størmer (3 September 1874 – 13 August 1957) was a Norwegian mathematician and astrophysicist. In mathematics, he is known for his work in number theory, including the calculation of

π

and Størmer's theorem on consecutive smooth numbers. In physics, he is known for studying the movement of charged particles in the magnetosphere and the formation of aurorae, and for his book on these subjects, From the Depths of Space to the Heart of the Atom. He worked for many years as a professor of mathematics at the University of Oslo in Norway. A crater on the far side of the Moon is named after him. (Full article...)

The graph of the 3-3 duoprism (the line graph of $K_{3,3}$ ) is perfect. Here it is colored with three colors, with one of its 3-vertex maximum cliques highlighted.

In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.

The perfect graphs include many important families of graphs and serve to unify results relating colorings and cliques in those families. For instance, in all perfect graphs, the graph coloring problem, maximum clique problem, and maximum independent set problem can all be solved in polynomial time, despite their greater complexity for non-perfect graphs. In addition, several important minimax theorems in combinatorics, including Dilworth's theorem and Mirsky's theorem on partially ordered sets, Kőnig's theorem on matchings, and the Erdős–Szekeres theorem on monotonic sequences, can be expressed in terms of the perfection of certain associated graphs. (Full article...)

In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.

An unsolved problem of Paul Erdős asks how many edges a unit distance graph on

n

vertices can have. The best known lower bound is slightly above linear in

n

—far from the upper bound, proportional to

n^{4/3}

. The number of colors required to color unit distance graphs is also unknown (the Hadwiger–Nelson problem): some unit distance graphs require five colors, and every unit distance graph can be colored with seven colors. For every algebraic number there is a unit distance graph with two vertices that must be that distance apart. According to the Beckman–Quarles theorem, the only plane transformations that preserve all unit distance graphs are the isometries. (Full article...)

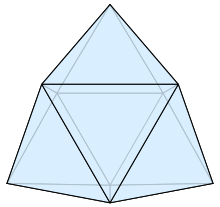
The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron, composite polyhedron, and Johnson solid.

The edges and vertices of the triaugmented triangular prism form a maximal planar graph with 9 vertices and 21 edges, called the Fritsch graph. It was used by Rudolf and Gerda Fritsch to show that Alfred Kempe's attempted proof of the four color theorem was incorrect. The Fritsch graph is one of only six graphs in which every neighborhood is a 4- or 5-vertex cycle. (Full article...)

In graph theory, the De Bruijn–Erdős theorem relates graph coloring of an infinite graph to the same problem on its finite subgraphs. It states that, when all finite subgraphs can be colored with

c

colors, the same is true for the whole graph. The theorem was proved by Nicolaas Govert de Bruijn and Paul Erdős (1951), after whom it is named.

The De Bruijn–Erdős theorem has several different proofs, all depending in some way on the axiom of choice. Its applications include extending the four-color theorem and Dilworth's theorem from finite graphs and partially ordered sets to infinite ones, and reducing the Hadwiger–Nelson problem on the chromatic number of the plane to a problem about finite graphs. It may be generalized from finite numbers of colors to sets of colors whose cardinality is a strongly compact cardinal. (Full article...)

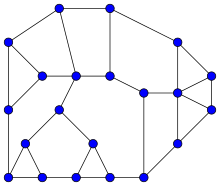
In graph theory, a Halin graph is a type of planar graph, constructed by connecting the leaves of a tree into a cycle.
The tree must have at least four vertices, none of which has exactly two neighbors; it should be drawn in the plane so none of its edges cross (this is called a planar embedding), and the cycle
connects the leaves in their clockwise ordering in this embedding. Thus, the cycle forms the outer face of the Halin graph, with the tree inside it.

Halin graphs are named after German mathematician Rudolf Halin, who studied them in 1971.
The cubic Halin graphs – the ones in which each vertex touches exactly three edges – had already been studied over a century earlier by Kirkman.
Halin graphs are polyhedral graphs, meaning that every Halin graph can be used to form the vertices and edges of a convex polyhedron, and the polyhedra formed from them have been called roofless polyhedra or domes. (Full article...)

In the mathematical field of graph theory, a graph homomorphism is a mapping between two graphs that respects their structure. More concretely, it is a function between the vertex sets of two graphs that maps adjacent vertices to adjacent vertices.

Homomorphisms generalize various notions of graph colorings and allow the expression of an important class of constraint satisfaction problems, such as certain scheduling or frequency assignment problems.
The fact that homomorphisms can be composed leads to rich algebraic structures: a preorder on graphs, a distributive lattice, and a category (one for undirected graphs and one for directed graphs).
The computational complexity of finding a homomorphism between given graphs is prohibitive in general, but a lot is known about special cases that are solvable in polynomial time. Boundaries between tractable and intractable cases have been an active area of research. (Full article...)

Kawasaki's theorem or Kawasaki–Justin theorem is a theorem in the mathematics of paper folding that describes the crease patterns with a single vertex that may be folded to form a flat figure. It states that the pattern is flat-foldable if and only if alternatingly adding and subtracting the angles of consecutive folds around the vertex gives an alternating sum of zero.
Crease patterns with more than one vertex do not obey such a simple criterion, and are NP-hard to fold.

The theorem is named after one of its discoverers, Toshikazu Kawasaki. However, several others also contributed to its discovery, and it is sometimes called the Kawasaki–Justin theorem or Husimi's theorem after other contributors, Jacques Justin and Kôdi Husimi. (Full article...)

In mathematics, the factorial of a non-negative integer

n

, denoted by

n!

, is the product of all positive integers less than or equal to

n

. The factorial of

n

also equals the product of

n

with the next smaller factorial:

<br>{\begin{aligned}n!&=n\times (n-1)\times (n-2)\times (n-3)\times \cdots \times 3\times 2\times 1\\<br>&=n\times (n-1)!\\<br>\end{aligned}}

For example,

5!=5\times 4!=5\times 4\times 3\times 2\times 1=120.

The value of 0! is 1, according to the convention for an empty product.

Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book Sefer Yetzirah. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of

n

distinct objects: there are

n!

. In mathematical analysis, factorials are used in power series for the exponential function and other functions, and they also have applications in algebra, number theory, probability theory, and computer science. (Full article...)

More good articles

Did you know (auto-generated) – load new batch

... that the word algebra is derived from an Arabic term for the surgical treatment of bonesetting?
... that circle packings in the form of a Doyle spiral were used to model plant growth long before their mathematical investigation by Doyle?
... that Ukrainian baritone Danylo Matviienko, who holds a master's degree in mathematics, appeared as Demetrius in Britten's opera A Midsummer Night's Dream at the Oper Frankfurt?
... that people in Madagascar perform algebra on tree seeds in order to tell the future?
... that in 1940 Xu Ruiyun became the first Chinese woman to receive a PhD in mathematics?
... that Catechumen, a Christian first-person shooter, was funded only in the aftermath of the Columbine High School massacre?
... that after Florida schools banned 54 mathematics books, Chaz Stevens petitioned that they also ban the Bible?
... that despite a mathematical model deeming the ice cream bar flavour Goody Goody Gum Drops impossible, it was still created?

edit

More did you know – view different entries

Did you know...

...that it is possible for a three-dimensional figure to have a finite volume but infinite surface area, such as Gabriel's Horn?
... that as the dimension of a hypersphere tends to infinity, its "volume" (content) tends to 0?
...that the primality of a number can be determined using only a single division using Wilson's Theorem?
...that the line separating the numerator and denominator of a fraction is called a solidus if written as a diagonal line or a vinculum if written as a horizontal line?
...that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type the complete works of William Shakespeare?
... that there are 115,200 solutions to the ménage problem of permuting six female-male couples at a twelve-person table so that men and women alternate and are seated away from their partners?
... that mathematician Paul Erdős called the Hadwiger conjecture, a still-open generalization of the four-color problem, "one of the deepest unsolved problems in graph theory"?

More did you know facts

Showing 7 items out of 75

edit

Selected article – show another

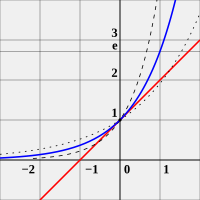e is the unique number such that the slope of y=e (blue curve) is exactly 1 when x=0 (illustrated by the red tangent line). For comparison, the curves y=2 (dotted curve) and y=4 (dashed curve) are shown.
Image credit: Dick Lyon

The mathematical constant e is occasionally called Euler's number after the Swiss mathematician Leonhard Euler, or Napier's constant in honor of the Scottish mathematician John Napier who introduced logarithms. It is one of the most important numbers in mathematics, alongside the additive and multiplicative identities 0 and 1, the imaginary unit i, and π, the circumference to diameter ratio for any circle. It has a number of equivalent definitions. One is given in the caption of the image to the right, and three more are:

The sum of the infinite series
${\begin{aligned}e&=\sum _{n=0}^{\infty }{\frac {1}{n!}}\\&={\frac {1}{0!}}+{\frac {1}{1!}}+{\frac {1}{2!}}+{\frac {1}{3!}}+\cdots \\\end{aligned}}$

where n! is the factorial of n, and 0! is defined to be 1 by convention.
The global maximizer of the function
$f(x)=x^{1 \over x}.$
The limit:
$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

The number e is also the base of the natural logarithm. Since e is transcendental, and therefore irrational, its value can not be given exactly. The numerical value of e truncated to 20 decimal places is 2.71828 18284 59045 23536. (Full article...)

View all selected articles

edit

Subcategories

Full category tree. Select [►] to view subcategories.

More mathematics categories

edit

Topics in mathematics

General	Foundations	Number theory	Discrete mathematics
Mathematicians History of mathematics Philosophy of mathematics Mathematical notation Mathematical beauty Mathematics education Glossary of mathematical symbols	Foundations of mathematics Mathematical logic Proof theory Gödel's incompleteness theorems Model theory Recursion theory Set theory Naive set theory Axiomatic set theory Category theory Topos theory	Number theory Algebraic number theory Analytic number theory Arithmetic Fundamental theorem of arithmetic Numbers Natural numbers Prime numbers Rational numbers Algebraic numbers	Discrete mathematics Combinatorics Combinatorial geometry Coding theory Combinatorial design Enumerative combinatorics Combinatorial optimization Graph theory Order theory Lattice theory Digital Signal Processing Theoretical computer science Computability theory Complexity theory
Algebra	Analysis	Geometry and topology	Applied mathematics
Algebra Elementary algebra Abstract algebra Group theory Ring theory Field theory Commutative algebra Geometric algebra Linear algebra Matrix theory Multilinear algebra Universal algebra Fundamental theorem of algebra	Analysis Calculus Fundamental theorem of calculus Vector calculus Geometric calculus Measure theory Real analysis Complex analysis Differential equations Ordinary differential equations Partial differential equations Integral equations Approximation theory Special functions Potential theory Harmonic analysis Fourier analysis Functional analysis Operator theory	Geometry Euclidean geometry Trigonometry Analytic geometry Non-Euclidean geometry Affine geometry Projective geometry Convex geometry Discrete geometry Algebraic geometry Differential geometry K theory Gauge theory Riemannian geometry Lie groups Topology General topology Algebraic topology Geometric topology Differential topology	Applied mathematics Mathematical modeling Mathematical physics Dynamical systems Control theory Calculus of variations Optimization Mathematical economics Game theory Mathematical finance Statistics Probability theory Stochastic processes Numerical analysis Cryptography Information theory

General

Foundations

Number theory

Discrete mathematics

Algebra

Analysis

Geometry and topology

Applied mathematics

edit

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z